SDGs
連携提案
この研究室では、可積分系に関する研究を行っている。これらは、主に理論物理や数理物理に現れる方程式だが、最近、連続可積分系の離散化等の研究から得られる専門的技術に基づいて、自然現象のセルオートマトンによるモデル化や解析に非常に有効な数学的手法を提案している。概略を言えば、まず、現象のマクロモデル、つまり常微分方程式や偏微分方程式によるモデルを立ててから、その方程式のある種の忠実な離散化を行う必要がある。その後、その離散系の「超離散極限」という変換によって、元の連続モデルと同じ振舞いを示しているセルオートマトンを系統的に得ることができる。今まで、この超離散化による手法を用いて、伝染病の流行モデルや免疫反応を記述する基本的なモデル、または様々な被食者・捕食者モデルに対応するセルオートマトンを得ることができた。本研究に関心を持つ企業等との共同研究が可能である。
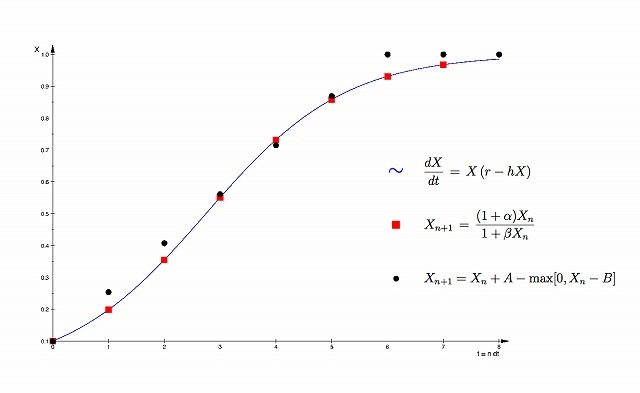
ロジスティック式の解とその離散化と超離散化
ロジスティック式の解(青線)と離散の Logistic 方程式の解(赤丸)またはその超離散化として得られたセルオートマトンの解(黒丸)
© WILLOX,Ralph